Sbírka úloh z fyziky
pro základní a střední školy
tíhové zrychlení ... g = 10 m∙s-2
měrná tepelná kapacita vody ... c = 4 200 J/(kg∙°C)
Faradayova konstanta ... F = 9,65·104 C·mol-1
permitivita vakua ... ε0 = 8,85·10-12C2·N-1·m-2
rychlost světla ve vakuu ... c = 3·108 m·s-1
elementární elektrický náboj ... e = 1,6·10-19 C
Planckova konstanta ... 6,63·10-34 J·s
hmotnost elektronu ... me = 9,1·10-31 kg
Stefanova-Boltzmannova konstanta ... σ = 5,67 ∙ 10-8 W∙m-2∙K-4
měrná tepelná kapacita vody ... c = 4 200 J/(kg∙°C)
Faradayova konstanta ... F = 9,65·104 C·mol-1
permitivita vakua ... ε0 = 8,85·10-12C2·N-1·m-2
rychlost světla ve vakuu ... c = 3·108 m·s-1
elementární elektrický náboj ... e = 1,6·10-19 C
Planckova konstanta ... 6,63·10-34 J·s
hmotnost elektronu ... me = 9,1·10-31 kg
Stefanova-Boltzmannova konstanta ... σ = 5,67 ∙ 10-8 W∙m-2∙K-4
Optika
Optika Na hladině jezera plove dřevěné kruhové pódium o průměru 15 m. Vypočítejte průměr plného stínu pod pódiem, jestliže jezero je zde hluboké 3,5 m. (Předpokládejme, že prostor nad vodní hladinou je osvětlen rozptýleným světlem.)
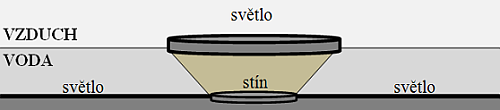
Řešení:
Při přechodu světelného paprsku z opticky řidšího prostředí (vzduch) do prostředí opticky hustšího (voda) nastává lom ke kolmici. Proto paprsky s úhlem dopadu 90° mají úhel lomu menší než 90°. (Na obrázku jsou tyto paprsky označeny jako paprsek A a paprsek B.) Proto do určité části prostoru pod dřevěným pódiem neproniká světlo.
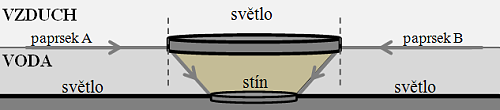
Nejprve vypočítáme, pod jakým úhlem se bude lámat paprsek A (popř. paprsek B):
α = 90°, β = ? °, n1 = 1, n2 = 1,33
Při výpočtu využijeme tzv. Snellův zákon lomu světla ve tvaru
Vyjádříme sin β
Číselně
S využitím hodnot ze zadání příkladu a vypočítané hodnoty úhlu β nyní vypočítáme jaký je průměr stínu d na dně jezera:
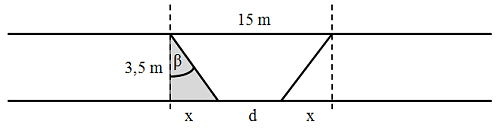
Číselně:
Odpověď:
Průměr plného stínu pod pódiem je přibližně 7 m.
